写在前面

做了一道大水题，挺有趣的，做不出来百度到可以使用树状数组或者线段树来解答，于是选择了实现起来比较简单的树状数组来解题。一开始思考了很久，想不通为啥可以使用树状数组就能解出来，逛了会b站回来就想通了（逆大天），在此感谢xenny大佬的树状数组详解，帮助我学习到了一个全新的知识点😇。

树状数组

先来谈谈树状数组：就是拿数组来模拟树形的结构，可以解决大部分区间更新以及求和的问题。

先看看具体的例子：

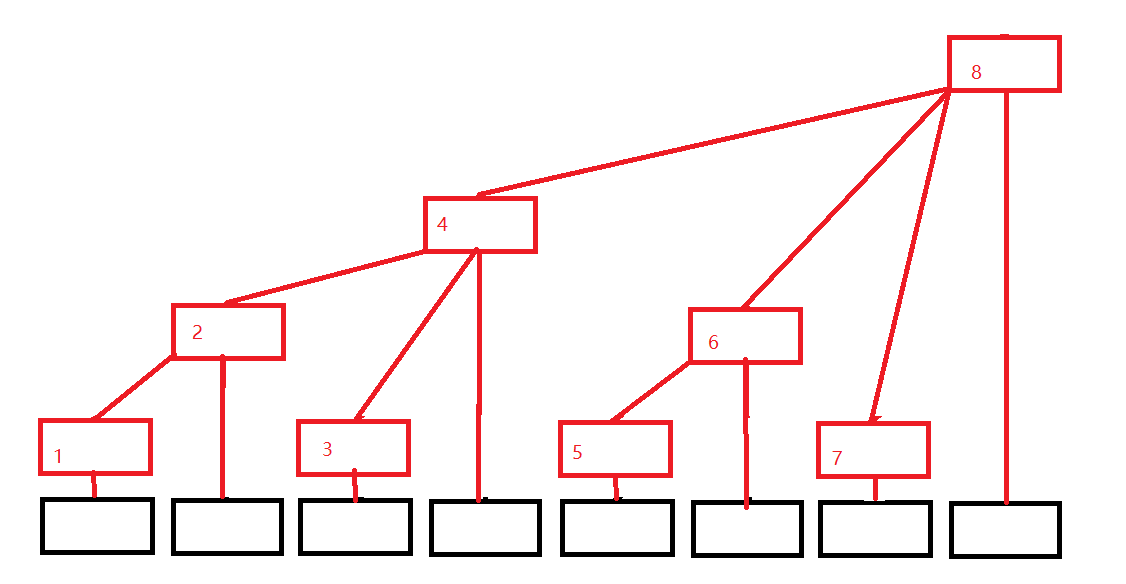
红色的为C[i]，黑色的为A[i]，关系式可以推出如下：

• C[1] = A[1];
• C[2] = A[1] + A[2];
• C[3] = A[3];
• C[4] = A[1] + A[2] + A[3] + A[4];
• C[5] = A[5];
• C[6] = A[5] + A[6];
• C[7] = A[7];
• C[8] = A[1] + A[2] + A[3] + A[4] + A[5] + A[6] + A[7] + A[8];

然后就自然而然可以推出来一些规律性的东西：

C[i] = A[i - 2^k+1] + A[i - 2^k+2] +…+ A[i]; (其中k为就是从最低位开始，第一个为1的2的指数)

又容易得出SUM（i） = C[i] + C[i-2^k（1）] + C[(i - 2^k（1）) - 2^k（2）] + …..；(k从2^0开始往上递增，直到c[i]不存在时)

然后就到了第一个难点，我第一个看不懂的地方： i&(-i);

翻阅树状数组的文章时才明白是前人的的智慧。。。2^k = i&(-i);

开始偷懒复制粘贴了

这里利用的负数的存储特性，负数是以补码存储的，对于整数运算 x&(-x)有 ● 当x为0时，即 0 & 0，结果为0； ●当x为奇数时，最后一个比特位为1，取反加1没有进位，故x和-x除最后一位外前面的位正好相反，按位与结果为0。结果为1。 ●当x为偶数，且为2的m次方时，x的二进制表示中只有一位是1（从右往左的第m+1位），其右边有m位0，故x取反加1后，从右到左第有m个0，第m+1位及其左边全是1。这样，x& (-x) 得到的就是x。 ●当x为偶数，却不为2的m次方的形式时，可以写作x= y * (2^k)。其中，y的最低位为1。实际上就是把x用一个奇数左移k位来表示。这时，x的二进制表示最右边有k个0，从右往左第k+1位为1。当对x取反时，最右边的k位0变成1，第k+1位变为0；再加1，最右边的k位就又变成了0，第k+1位因为进位的关系变成了1。左边的位因为没有进位，正好和x原来对应的位上的值相反。二者按位与，得到：第k+1位上为1，左边右边都为0。结果为2^k。 总结一下：x&(-x)，当x为0时结果为0；x为奇数时，结果为1；x为偶数时，结果为x中2的最大次方的因子。

而且这个有一个专门的称呼，叫做lowbit，即取2^k。

下面就贴贴代码模板了：

#include <bits/stdc++.h>
using namespace std;

int n,m;
int a[50005],c[50005]; //对应原数组和树状数组

int lowbit(int x){
    return x&(-x);
}

void updata(int i,int k){    //在i位置加上k
    while(i <= n){
        c[i] += k;
        i += lowbit(i);
    }
}

int getsum(int i){        //求A[1 - i]的和
    int res = 0;
    while(i > 0){
        res += c[i];
        i -= lowbit(i);
    }
    return res;
}

int main(){
    int t;
    cin>>t;
    for(int tot = 1; tot <= t; tot++){
        cout << "Case " << tot << ":" << endl;
        memset(a, 0, sizeof a);
        memset(c, 0, sizeof c);
        cin>>n;
        for(int i = 1; i <= n; i++){
            cin>>a[i];
            updata(i,a[i]);   //输入初值的时候，也相当于更新了值
        }

        string s;
        int x,y;
        while(cin>>s && s[0] != 'E'){
            cin>>x>>y;
            if(s[0] == 'Q'){    //求和操作
                int sum = getsum(y) - getsum(x-1);    //x-y区间和也就等于1-y区间和减去1-(x-1)区间和
                cout << sum << endl;
            }
            else if(s[0] == 'A'){
                updata(x,y);
            }
            else if(s[0] == 'S'){
                updata(x,-y);    //减去操作，即为加上相反数
            }
        }

    }
    return 0;
}

关于树状数组的变形，有时间再写吧（可能不会再写了，毕竟就是学这一段时间

————————————————

原题目

题目竟然叫作这是一道大水题，焯😡

对应AC的代码：

#include<bits/stdc++.h> 
using namespace std;
typedef long long ll;
ll a[300005],c[300005]={0};
ll n,m;
ll result=0;
inline ll read()
{
	int x=0,f=1;char ch=getchar();
    while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
    while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
    return x*f;
}
ll lowbit(ll x)
{
	return x&(-x);
}
void update(ll i,ll value)
{
	while(i<=n)
	{
		c[i]+=value;
		i+=lowbit(i);
	}
}
ll getsum(ll i )
{
	ll sum=0;
	while(i>0)
	{
		sum+=c[i];
		i-=lowbit(i);
	}
	return sum;
}
int main()
{
	n=read();
	m=read();
	while(m--)
	{
		ll c;
		c=read();
		if(c==0)
		{
			ll left,right,value;
			left=read();right=read();value=read();
			ll temp=(right-left+1)*value;
			result+=temp;
			update(left,temp);
			update(right+1,-temp);
		}
		else 
		{
			ll pos;
			pos=read();
			cout<<result-getsum(pos)<<endl;
		}
	 } 
	 return 0;
}